广义相对论与微分几何(一):微分流形

流形

定义一(n维流形)
拓扑空间$(M,\mathscr{F})$称为$n$维微分流形, 若$M$有开覆盖$\{O_{\alpha}\}$满足:

• 每一个$O_\alpha$, $\exist$同胚映射$\psi_\alpha:O_\alpha\rightarrow V_\alpha$, 其中$V_\alpha$为$\R^n$的开子集
• 若$O_\alpha\cap O_\beta\ne\emptyset$, 则$\psi_\beta\circ\psi_\alpha^-1$是光滑的

其中, 上面的第二条称为相容性条件.

图册

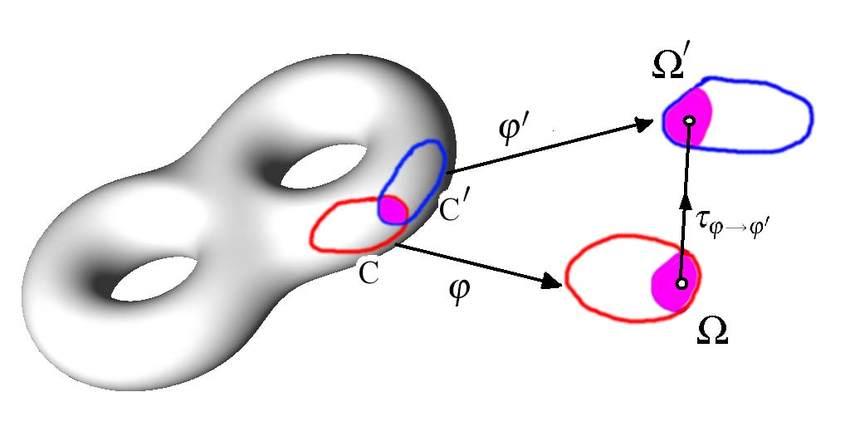
定义二(图, 图册, 坐标系)
一个$(O_\alpha,\psi_\alpha)$称为一个(局域)坐标系, $O_\alpha$称为坐标域.
坐标系$(O_\alpha,\psi_\alpha)$在数学上又叫图, 满足定义一的开覆盖的图的集合$\{(O_\alpha,\psi_\alpha)\}$称为图册.

定义三(微分结构)
对于拓扑空间$M$上的两个图册$\{(O_\alpha,\psi_\alpha)\}$与$\{(O_\beta,\psi_\beta)\}$:

• 若两个图册不相容, 则称两个图册把$M$定义为两个不同的微分结构
• 若两个图册相容, 则将其合并为同一个图册, 我们总是选择最大的图册讨论.

定义四(流形上的映射)
设$M$与$M'$分别为$n$与$n'$维的流形, $\{(O_\alpha,\psi_\alpha)\}$与$\{(O'_\alpha,\psi'_\alpha)\}$为两者的图册.
令$f:M\rightarrow M'$为流形上的映射, 则$f$称为$C^r$类映射若$\forall p\in M$, $\psi_\beta'\circ f\circ\psi^{-1}_\alpha$为$C^r$类映射.

定义五(微分同胚)
流形$M$与$M'$为互相微分同胚的, 若$\exist f:M\rightarrow M'$, 满足:

• $f$为双射(即一一映射)
• $f$与$f^{-1}$为$C^{\infty}$的