其实这一篇将其称为什么是量子力学中的量子更为恰当, 但由于想到这个问题是在如何将一个经典电磁场量子化为量子场论中的对象, 因此就用了这个标题. 不过我们硬要深究这个标题中量子化的含义的话, 其实仅仅是想表达如何理解那些经典和量子上的联系. 本文主要想探讨的是从纯逻辑直观的角度上来看, 给出为什么量子化的理论是一个相比经典理论更加基本普适的理论, 以及其与经典的联系.

物理态的抽象提出

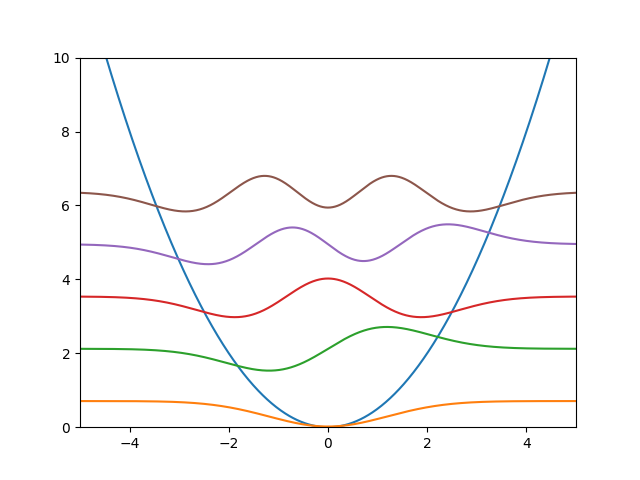
为了达到我们的目标, 我们必须先能够在直觉上感受到物理态这个概念. 我们不妨想象一个运动在谐振子势(也就是常说的二次函数)下的非零质量单粒子系统:
谐振子势
当我们在讨论时刻tt的系统时, 我们究竟是在讨论什么呢? 在经典上, 我们会说:“诶呀, 肯定是这系统中的那个粒子的位置喽, 知道了那玩意的演化性质我们不就能分析一堆统计性质了嘛!” 是的, 我们在经典中大多都会按x(t)x(t)来描述这个系统的性质. 但这时候, 可能有些了解微分方法的人就会说:“欸, 那其实假若我知道vv的信息也是行的嘛, 反正知晓初始位置, 我们总能求得xx的.” 当然类似地, 也会有一些ODE学的很好的, 或者了解过相空间的人会说:"诶呀, 物理系统是由哈密顿系统来描述, 而哈密顿系统由于其基流形将我们物理系统的状态完全包含而不需要其上的纤维, 因此我们应该说从相空间的角度来看这个物理系统. 同时, 这个相空间描述还能将系统的演化抽象为其上的轨道, 有很多良好的性质啊! " 就这样, 大家百家争鸣, 但描述的都是一开始提到的谐振子势溪西岸的系统.但是, 当我们远离这些说法, 再去思考开头抛出的问题, 对于一个系统, 我们讨论的究竟是什么呢? 我们前面的几种描述方法都可行, 但是什么导致了它的差异呢? 我们会发现, 我们虽然讨论的都是同一个系统内部的状态, 但我们在观测的量上出现了差别: 有的人选择了x^\hat{x}, 有的人选择了v^\hat{v}, 有的人选择了x^\hat{x}和p^\hat{p}. 他们之间的共同点在于都成功描述了系统的状态.

这似乎能够给我们启示, 既然我们描述的东西都是同一个系统的同一个状态, 而我们平常表述它又一定要指定某个"坐标系"(这里提及的坐标系仅是一个概念类比, 类比我们在讨论流形时总要指定一个局域坐标系才最终进行分析运算), 那我们不妨将系统态这个概念从具体的"坐标系"中抽离开来, 给予它一个记号∣ψ⟩\ket{\psi}. 当我们用某些"坐标系"(观测量)来描述它在某时的状态时, 记为A^∣ψ⟩\hat{A}\ket{\psi}, 而又当我们期望总能让∣ψ⟩\ket{\psi}在某一个"全局坐标系"按照一个固定种类的观测量A^\hat{A}被标记时, 我们称选取了一个表象, 记为⟨A∣∣ψ⟩\bra{A}\ket{\psi}, 这也就是常提到的表象下的表示. 一个最常见的例子就是当我们选取x^\hat{x}作为全局观测量时, 这个⟨x∣∣ψ⟩\bra{x}\ket{\psi}称为位置表象下的波函数ψ(x)\psi(x).

到这里, 我们想必能够看出来, 量子理论将物理态这个概念抽象了出来, 无疑时一次理论概念上的创新!

经典观测的算符表示带来的量子体现

在讲完前面提及的物理态的抽象凝练后, 我们就能够比较畅快地感受到量子这个概念体现在哪里了.

我们在前面提到, 当我们需要对物理态进行观测时, 我们必然定义了能够对物理态产生影响的观测方法A^\hat{A}, 其左作用在∣ψ⟩\ket{\psi}上满足:

A^∣ψ⟩=∣ψ′⟩\hat{A}\ket{\psi}=\ket{\psi'}

此处地∣ψ′⟩\ket{\psi'}表示的也是该系统中一个可能的态, 也许你会好奇为什么∣ψ′⟩\ket{\psi'}还是系统的态, 这是因为我们对系统的描述隐含了"观测者加入"的条件, 因此我们的观测后仍然是系统的态应该是比较自然的了.

我们从上面的定义中还能发现一件事情, 我们定义的观测方法A^\hat{A}实际上在就对应着数学中的线性算符的概念, 这一点的发现让我们能够直接和数学理论挂起钩, 能够方便快捷地讨论这些算符的性质以及它对态产生的影响.

Hilbert空间表述

一个首先能够看出的性质是∣ψ⟩\ket{\psi}的 Hilbert\mathscr{H}ilbert空间表述, 告诉了我们∣ψ⟩\ket{\psi}在算符下拥有本征值以及更多相关的结论, 我们也终于能够明着来定义本征态的结论了. 即对于算符A^\hat{A}, 其拥有本征态∣ψA⟩\ket{\psi_A}满足:

A^∣ψA⟩=a∣ψA⟩\hat{A}\ket{\psi_A}=a\ket{\psi_A}

算符的建立

当然, 还有与 PoincarePoincare群, SO(3)\mathbf{SO}(3)或SO(3,1)\mathbf{SO}(3,1)对称性带来的动量算符P^\hat{P}, 角动量算符J^\hat{J}以及联系着时间平移变换的算符H^\hat{H}.

量子(离散性质)的起源

总而言之, 现在我们定义了这么多的算符, 其中有一个极其容易发生的事情就是算符之间的对易关系. 这么多算符, 它们之间非常容易不对易啊, 或者物理上说就是观测到的结果和你的顺序(这里提及的顺序可能有用词错误, 但其中表述的含义应该是一致的)有关啊! 这极大地限制了我们能够进行的观测种类, 而且这是对理论算符化后必然带来的特征.

同样的, 由于这个不对易性质, 我们能够发现观测值收到了大量限制, 我们物理态∣ψ⟩\ket{\psi}在某些算符下的可能观测值在很大一部分系统中将不再连续, 而是离散的, 这也就是所谓量子效应的起源.
一个经典例子就是我们前面提及的谐振子下的允许能级将变为En=(n+12)ℏωE_n=(n+\frac{1}{2})\hbar\omega.
谐振子下的离散能谱